Neu: Zum Ausprobieren gibt es hier eine Rechentablett-Webapp mit reduziertem Funktionsumfang.
Mit der App Rechentablett für iOS (iPad und iPhone/iPod Touch) kann das Teile-Ganzes-Konzept, welches den Grundoperationen Plus und Minus zugrunde liegt, veranschaulicht und interaktiv erforscht werden. Die Idee für dieses virtuelle Arbeitsmittel entstand auf Grundlage der Überlegungen von Gerster & Schultz (2000) zur Förderung des Teile-Ganzes-Verständnisses bei Kindern mit Rechenschwierigkeiten.
Beschreibung der App
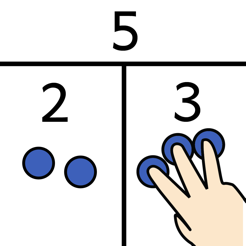
Zwei (Teil-)Mengen geben zusammen eine Menge. Das nennt man Plusrechnen. Und wenn du von einer Menge einen Teil wegnimmst, bleibt ein anderer Teil übrig. Das nennt man dann Minusrechnen. Mit diesem Arbeitsmittel kannst du diese Zusammenhänge zwischen Teilmengen und Gesamtmenge interaktiv erfahren und erforschen.
- Berühre mit deinen Fingern den Bildschirm, um ein oder mehrere Plättchen zu legen oder sie von einer Seite zur anderen zu verschieben.
- Streiche über eine Zahl, um sie aus- oder wieder einzublenden.
- Tippe auf eine Zahl, um die Plättchen auf dem Feld zu sortieren.
- Ziehe den Rolladen runter und wieder hoch, um eine Tabletthälfte abzudecken. So kannst du Aufgaben für deinen Lernpartner erstellen oder die Aufgabe kontrollieren.
- Ziehe ein Plättchen nach oben, um es zu löschen. Wenn du das Tablett schüttelst, wird es geleert.
Didaktische Grundlagen und beispielhafte Aufgabenstellungen
Die Grundoperationen Plus und Minus basieren auf dem Konzept, dass sich eine Menge in Teilmengen zerlegen lässt und sich Teilmengen wieder zusammenfügen lassen (Teile-Ganzes-Konzept). Bei der Addition werden zwei Teilmengen vereinigt zu einer Gesamtmenge. Bei der Subtraktion wird von einer Menge eine Teilmenge entfernt und es bleibt eine weitere Teilmenge übrig. Haben Kinder diese Beziehungen zwischen Teilmengen und Gesamtmenge verstanden, ist ein wesentlicher Grundstein für erfolgreiches mathematisches Lernen gelegt und die Voraussetzung dafür geschaffen, effektive Rechenstrategien zu entwickeln. Dieses virtuelle Arbeitsmittel stellt ein Hilfsmittel dar, mit dem sich das Teile-Ganzes-Konzept veranschaulichen, erleben und erforschen lässt.
Damit mit dem Lernmittel das Teile-Ganzes-Verständnis effektiv gefördert wird, bedarf es passender Aufgabenstellungen, die zum Experimentieren und Nachdenken mit dem Arbeitsmittel herausfordern. Besonders gut sind Aufgaben geeignet, die zum Entdecken von Zusammenhängen herausfordern (operative Aufgabenstellungen). Passende Aufgaben sind beispielsweise:
- Wie kannst du mit deinen Händen möglichst schnell 6 Plättchen auf das Tablett legen?
- Wie kannst du die Plättchen so anordnen, dass du möglichst schnell ohne Abzählen siehst wie viele es sind?
- Auf der einen Seite liegen 4 Plättchen, auf der anderen Seite 3 Plättchen. Wie viele Plättchen liegen auf beiden Seiten zusammen? (Addition)
- Was passiert, wenn ich 1 (2, 3, …) Plättchen von einer Seite auf die andere schiebe? (Zahlzerlegungen, Invarianz)
- Was passiert mit den Teilmengen und mit der Gesamtmenge, wenn ich ich ein Plättchen vom Tablett entferne?
- Wie viele verschiedene Möglichkeiten gibt es, 10 Plättchen auf beide Seiten zu verteilen? (Zahlzerlegung)
- Auf der einen Seite liegen 3 Plättchen. Wie viele muss ich auf der anderen Seite dazu legen, damit zusammen 7 Plättchen auf dem Tablett liegen? (Ergänzungsaufgaben)
- Auf dem Tablett liegen 10 Plättchen. Nur einen Teil kannst du sehen. Wie viele Plättchen sind verdeckt? (Ergänzen einer Menge, Subtraktion)
- Ich lege 8 Plättchen auf die eine Hälfte des Tabletts. Von den 8 Plättchen nehme ich nun 5 weg auf die andere Seite. Wie viele bleiben übrig? (Subtraktion)
- Auf dem Tablett liegt die Aufgabe 9 + 7. Wie kann ich die Plättchen so umlegen, dass ich sofort sehen kann, was heraus kommt? (Nachbaraufgaben als Rechenvorteil nutzen)
- Für die Einführung von Zahlenmauern oder bei Schwierigkeiten lässt sich das Rechentablett ebenfalls gut einsetzen, um die Zusammenhänge zu verdeutlichen.
Literatur
Gerster, H.-D & Schultz, Rita: Schwierigkeiten beim Erwerb mathematischer Konzepte im Anfangsunterricht (Forschungsbericht). Im Internet verfügbar unter: http://nbn-resolving.de/urn:nbn:de:bsz:frei129-opus-161